MultiLR: Prediction + inferential models

STA 210 - Spring 2022

Dr. Mine Çetinkaya-Rundel

Welcome

Topics

  • Predictions
  • Model selection
  • Checking conditions

Computational setup

# load packages
library(tidyverse)
library(tidymodels)
library(NHANES)
library(knitr)
library(patchwork)
library(colorblindr)
library(pROC)
library(Stat2Data)
library(nnet)

# set default theme and larger font size for ggplot2
ggplot2::theme_set(ggplot2::theme_minimal(base_size = 20))

NHANES Data

  • National Health and Nutrition Examination Survey is conducted by the National Center for Health Statistics (NCHS).
  • The goal is to “assess the health and nutritional status of adults and children in the United States”.
  • This survey includes an interview and a physical examination.

Variables

Goal: Use a person’s age and whether they do regular physical activity to predict their self-reported health rating.

  • Outcome: HealthGen: Self-reported rating of participant’s health in general. Excellent, Vgood, Good, Fair, or Poor.

  • Predictors:

    • Age: Age at time of screening (in years). Participants 80 or older were recorded as 80.
    • PhysActive: Participant does moderate to vigorous-intensity sports, fitness or recreational activities.

The data

nhanes_adult <- NHANES %>%
  filter(Age >= 18) %>%
  select(HealthGen, Age, PhysActive, Education) %>%
  drop_na() %>%
  mutate(obs_num = 1:n())
glimpse(nhanes_adult)
Rows: 6,465
Columns: 5
$ HealthGen  <fct> Good, Good, Good, Good, Vgood, Vgood, Vgood, Vgood, Vgood, …
$ Age        <int> 34, 34, 34, 49, 45, 45, 45, 66, 58, 54, 50, 33, 60, 56, 56,…
$ PhysActive <fct> No, No, No, No, Yes, Yes, Yes, Yes, Yes, Yes, Yes, No, No, …
$ Education  <fct> High School, High School, High School, Some College, Colleg…
$ obs_num    <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, …

Model in R

health_fit <- multinom_reg() %>%
  set_engine("nnet") %>%
  fit(HealthGen ~ Age + PhysActive, data = nhanes_adult)

health_fit <- repair_call(health_fit, data = nhanes_adult)

Model summary

tidy(health_fit) %>% print(n = 12)
# A tibble: 12 × 6
   y.level term            estimate std.error statistic  p.value
   <chr>   <chr>              <dbl>     <dbl>     <dbl>    <dbl>
 1 Vgood   (Intercept)    1.27        0.154      8.23   1.80e-16
 2 Vgood   Age           -0.0000361   0.00259   -0.0139 9.89e- 1
 3 Vgood   PhysActiveYes -0.332       0.0949    -3.50   4.72e- 4
 4 Good    (Intercept)    1.99        0.150     13.3    2.81e-40
 5 Good    Age           -0.00304     0.00256   -1.19   2.35e- 1
 6 Good    PhysActiveYes -1.01        0.0921   -11.0    4.80e-28
 7 Fair    (Intercept)    1.03        0.174      5.94   2.89e- 9
 8 Fair    Age            0.00113     0.00302    0.373  7.09e- 1
 9 Fair    PhysActiveYes -1.66        0.109    -15.2    4.14e-52
10 Poor    (Intercept)   -1.34        0.299     -4.47   7.65e- 6
11 Poor    Age            0.0193      0.00505    3.83   1.30e- 4
12 Poor    PhysActiveYes -2.67        0.236    -11.3    1.20e-29

Predictions

Calculating probabilities

  • For categories \(2,\ldots,K\), the probability that the \(i^{th}\) observation is in the \(j^{th}\) category is

    \[ \hat{\pi}_{ij} = \frac{e^{\hat{\beta}_{0j} + \hat{\beta}_{1j}x_{i1} + \dots + \hat{\beta}_{pj}x_{ip}}}{1 + \sum\limits_{k=2}^K e^{\hat{\beta}_{0k} + \hat{\beta}_{1k}x_{i1} + \dots \hat{\beta}_{pk}x_{ip}}} \]

  • For the baseline category, \(k=1\), we calculate the probability \(\hat{\pi}_{i1}\) as

    \[ \hat{\pi}_{i1} = 1- \sum\limits_{k=2}^K \hat{\pi}_{ik} \]

Predicted health rating

We can use our model to predict a person’s perceived health rating given their age and whether they exercise.

health_aug <- augment(health_fit, new_data = nhanes_adult)
health_aug
# A tibble: 6,465 × 11
   HealthGen   Age PhysActive Education      obs_num .pred_class .pred_Excellent
   <fct>     <int> <fct>      <fct>            <int> <fct>                 <dbl>
 1 Good         34 No         High School          1 Good                 0.0687
 2 Good         34 No         High School          2 Good                 0.0687
 3 Good         34 No         High School          3 Good                 0.0687
 4 Good         49 No         Some College         4 Good                 0.0691
 5 Vgood        45 Yes        College Grad         5 Vgood                0.155 
 6 Vgood        45 Yes        College Grad         6 Vgood                0.155 
 7 Vgood        45 Yes        College Grad         7 Vgood                0.155 
 8 Vgood        66 Yes        Some College         8 Vgood                0.157 
 9 Vgood        58 Yes        College Grad         9 Vgood                0.156 
10 Fair         54 Yes        9 - 11th Grade      10 Vgood                0.156 
# … with 6,455 more rows, and 4 more variables: .pred_Vgood <dbl>,
#   .pred_Good <dbl>, .pred_Fair <dbl>, .pred_Poor <dbl>

Actual vs. predicted health rating

For each observation, the predicted perceived health rating is the category with the highest predicted probability.

health_aug %>% select(contains("pred"))
# A tibble: 6,465 × 6
   .pred_class .pred_Excellent .pred_Vgood .pred_Good .pred_Fair .pred_Poor
   <fct>                 <dbl>       <dbl>      <dbl>      <dbl>      <dbl>
 1 Good                 0.0687       0.243      0.453     0.201     0.0348 
 2 Good                 0.0687       0.243      0.453     0.201     0.0348 
 3 Good                 0.0687       0.243      0.453     0.201     0.0348 
 4 Good                 0.0691       0.244      0.435     0.205     0.0467 
 5 Vgood                0.155        0.393      0.359     0.0868    0.00671
 6 Vgood                0.155        0.393      0.359     0.0868    0.00671
 7 Vgood                0.155        0.393      0.359     0.0868    0.00671
 8 Vgood                0.157        0.400      0.342     0.0904    0.0102 
 9 Vgood                0.156        0.397      0.349     0.0890    0.00872
10 Vgood                0.156        0.396      0.352     0.0883    0.00804
# … with 6,455 more rows

Confusion matrix

health_conf <- health_aug %>% 
  count(HealthGen, .pred_class, .drop = FALSE) %>%
  pivot_wider(names_from = .pred_class, values_from = n)

health_conf
# A tibble: 5 × 6
  HealthGen Excellent Vgood  Good  Fair  Poor
  <fct>         <int> <int> <int> <int> <int>
1 Excellent         0   528   210     0     0
2 Vgood             0  1341   743     0     0
3 Good              0  1226  1316     0     0
4 Fair              0   296   625     0     0
5 Poor              0    24   156     0     0

Actual vs. predicted health rating

Why do you think no observations were predicted to have a rating of “Excellent”, “Fair”, or “Poor”?

Model selection for inference

Comparing nested models

  • Suppose there are two models:
    • Reduced model includes predictors \(x_1, \ldots, x_q\)
    • Full model includes predictors \(x_1, \ldots, x_q, x_{q+1}, \ldots, x_p\)
  • We want to test the following hypotheses:
    • \(H_0: \beta_{q+1} = \dots = \beta_p = 0\)
    • \(H_A: \text{ at least 1 }\beta_j \text{ is not } 0\)
  • To do so, we will use the drop-in-deviance test (very similar to logistic regression)

Add Education to the model?

  • We consider adding the participants’ Education level to the model.
    • Education takes values 8thGrade, 9-11thGrade, HighSchool, SomeCollege, and CollegeGrad
  • Models we’re testing:
    • Reduced model: Age, PhysActive
    • Full model: Age, PhysActive, Education

\[ \begin{align} &H_0: \beta_{9-11thGrade} = \beta_{HighSchool} = \beta_{SomeCollege} = \beta_{CollegeGrad} = 0\\ &H_a: \text{ at least one }\beta_j \text{ is not equal to }0 \end{align} \]

Add Education to the model?

reduced_fit <- multinom_reg() %>%
  set_engine("nnet") %>%
  fit(HealthGen ~ Age + PhysActive,
  data = nhanes_adult)

full_fit <- multinom_reg() %>%
  set_engine("nnet") %>%
  fit(HealthGen ~ Age + PhysActive + Education,
  data = nhanes_adult)
  
reduced_fit <- repair_call(reduced_fit, data = nhanes_adult)
full_fit <- repair_call(full_fit, data = nhanes_adult)

Add Education to the model?

anova(reduced_fit$fit, full_fit$fit, test = "Chisq") %>%
  kable(digits = 3)
Model Resid. df Resid. Dev Test Df LR stat. Pr(Chi)
Age + PhysActive 25848 16994.23 NA NA NA
Age + PhysActive + Education 25832 16505.10 1 vs 2 16 489.132 0

At least one coefficient associated with Education is non-zero. Therefore, we will include Education in the model.

Model with Education

tidy(full_fit, conf.int = T) %>% print(n = 28)
# A tibble: 28 × 8
   y.level term         estimate std.error statistic  p.value conf.low conf.high
   <chr>   <chr>           <dbl>     <dbl>     <dbl>    <dbl>    <dbl>     <dbl>
 1 Vgood   (Intercept)   5.82e-1   0.301      1.93   5.36e- 2 -0.00914   1.17   
 2 Vgood   Age           1.12e-3   0.00266    0.419  6.75e- 1 -0.00411   0.00634
 3 Vgood   PhysActiveY… -2.64e-1   0.0985    -2.68   7.33e- 3 -0.457    -0.0711 
 4 Vgood   Education9 …  7.68e-1   0.308      2.49   1.27e- 2  0.164     1.37   
 5 Vgood   EducationHi…  7.01e-1   0.280      2.51   1.21e- 2  0.153     1.25   
 6 Vgood   EducationSo…  7.88e-1   0.271      2.90   3.71e- 3  0.256     1.32   
 7 Vgood   EducationCo…  4.08e-1   0.268      1.52   1.28e- 1 -0.117     0.933  
 8 Good    (Intercept)   2.04e+0   0.272      7.51   5.77e-14  1.51      2.57   
 9 Good    Age          -1.72e-3   0.00263   -0.651  5.15e- 1 -0.00688   0.00345
10 Good    PhysActiveY… -7.58e-1   0.0961    -7.88   3.16e-15 -0.946    -0.569  
11 Good    Education9 …  3.60e-1   0.275      1.31   1.90e- 1 -0.179     0.899  
12 Good    EducationHi…  8.52e-2   0.247      0.345  7.30e- 1 -0.399     0.569  
13 Good    EducationSo… -1.13e-2   0.239     -0.0472 9.62e- 1 -0.480     0.457  
14 Good    EducationCo… -8.91e-1   0.236     -3.77   1.65e- 4 -1.35     -0.427  
15 Fair    (Intercept)   2.12e+0   0.288      7.35   1.91e-13  1.55      2.68   
16 Fair    Age           3.35e-4   0.00312    0.107  9.14e- 1 -0.00578   0.00645
17 Fair    PhysActiveY… -1.19e+0   0.115    -10.4    3.50e-25 -1.42     -0.966  
18 Fair    Education9 … -2.24e-1   0.279     -0.802  4.22e- 1 -0.771     0.323  
19 Fair    EducationHi… -8.32e-1   0.252     -3.31   9.44e- 4 -1.33     -0.339  
20 Fair    EducationSo… -1.34e+0   0.246     -5.46   4.71e- 8 -1.82     -0.861  
21 Fair    EducationCo… -2.51e+0   0.253     -9.91   3.67e-23 -3.00     -2.01   
22 Poor    (Intercept)  -2.00e-1   0.411     -0.488  6.26e- 1 -1.01      0.605  
23 Poor    Age           1.79e-2   0.00509    3.53   4.21e- 4  0.00797   0.0279 
24 Poor    PhysActiveY… -2.27e+0   0.242     -9.38   6.81e-21 -2.74     -1.79   
25 Poor    Education9 … -3.60e-1   0.353     -1.02   3.08e- 1 -1.05      0.332  
26 Poor    EducationHi… -1.15e+0   0.334     -3.44   5.86e- 4 -1.81     -0.494  
27 Poor    EducationSo… -1.07e+0   0.316     -3.40   6.77e- 4 -1.69     -0.454  
28 Poor    EducationCo… -2.32e+0   0.366     -6.34   2.27e-10 -3.04     -1.60

Compare NHANES models using AIC

Reduced model:

glance(reduced_fit)$AIC
[1] 17018.23

Full model:

glance(full_fit)$AIC
[1] 16561.1

Checking conditions for inference

Conditions for inference

We want to check the following conditions for inference for the multinomial logistic regression model:

  1. Linearity: Is there a linear relationship between the log-odds and the predictor variables?

  2. Randomness: Was the sample randomly selected? Or can we reasonably treat it as random?

  3. Independence: Are the observations independent?

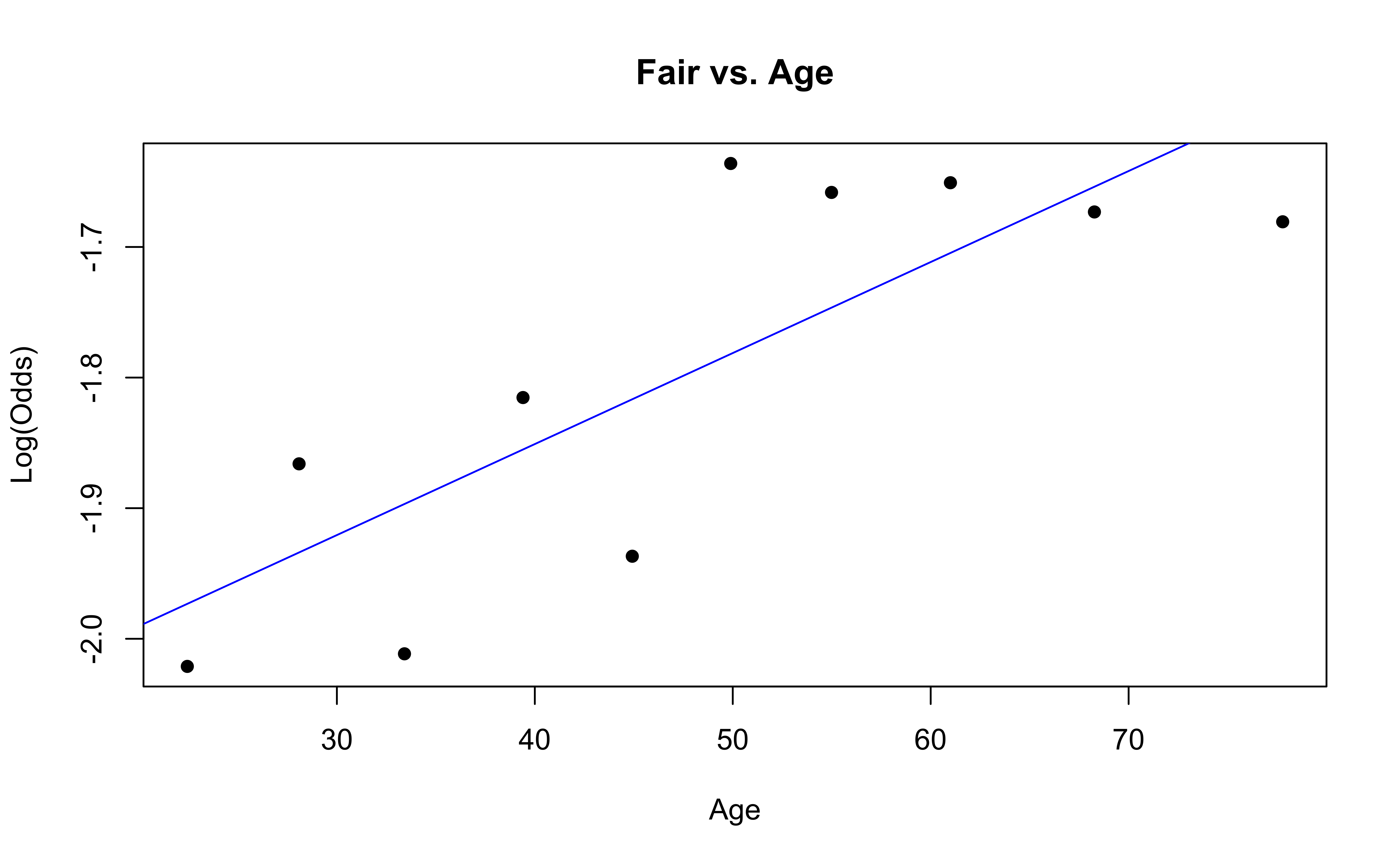
Checking linearity

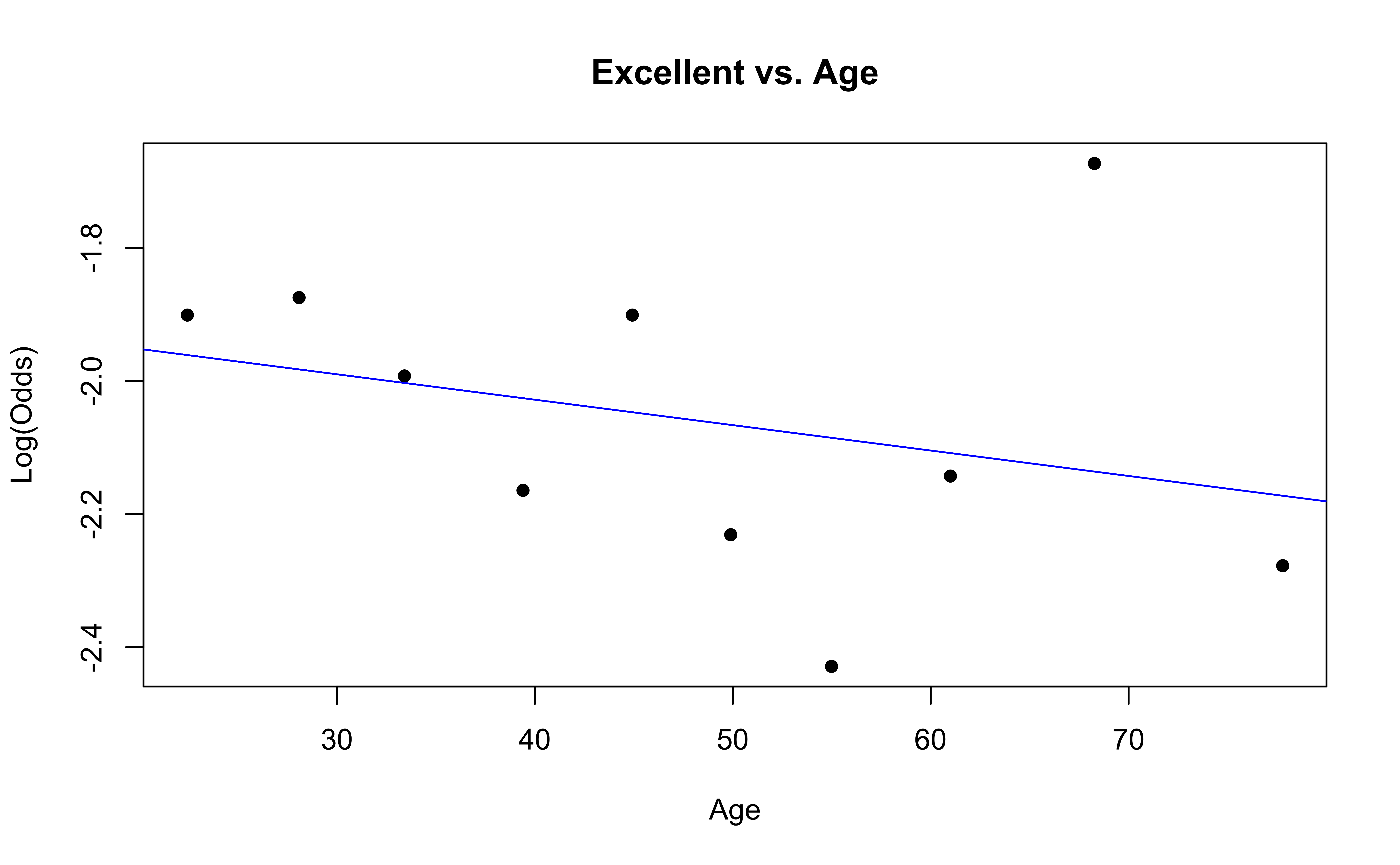
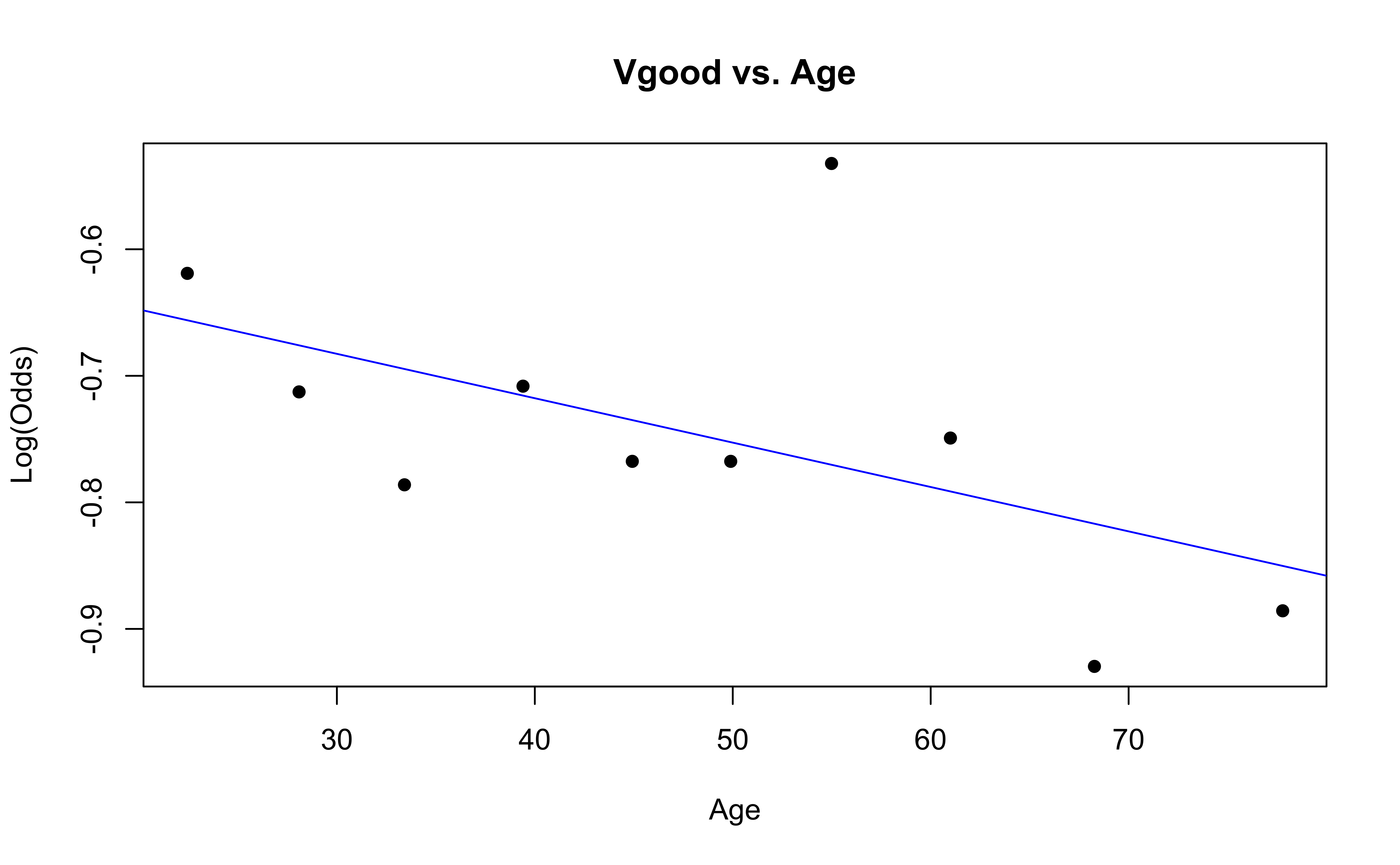
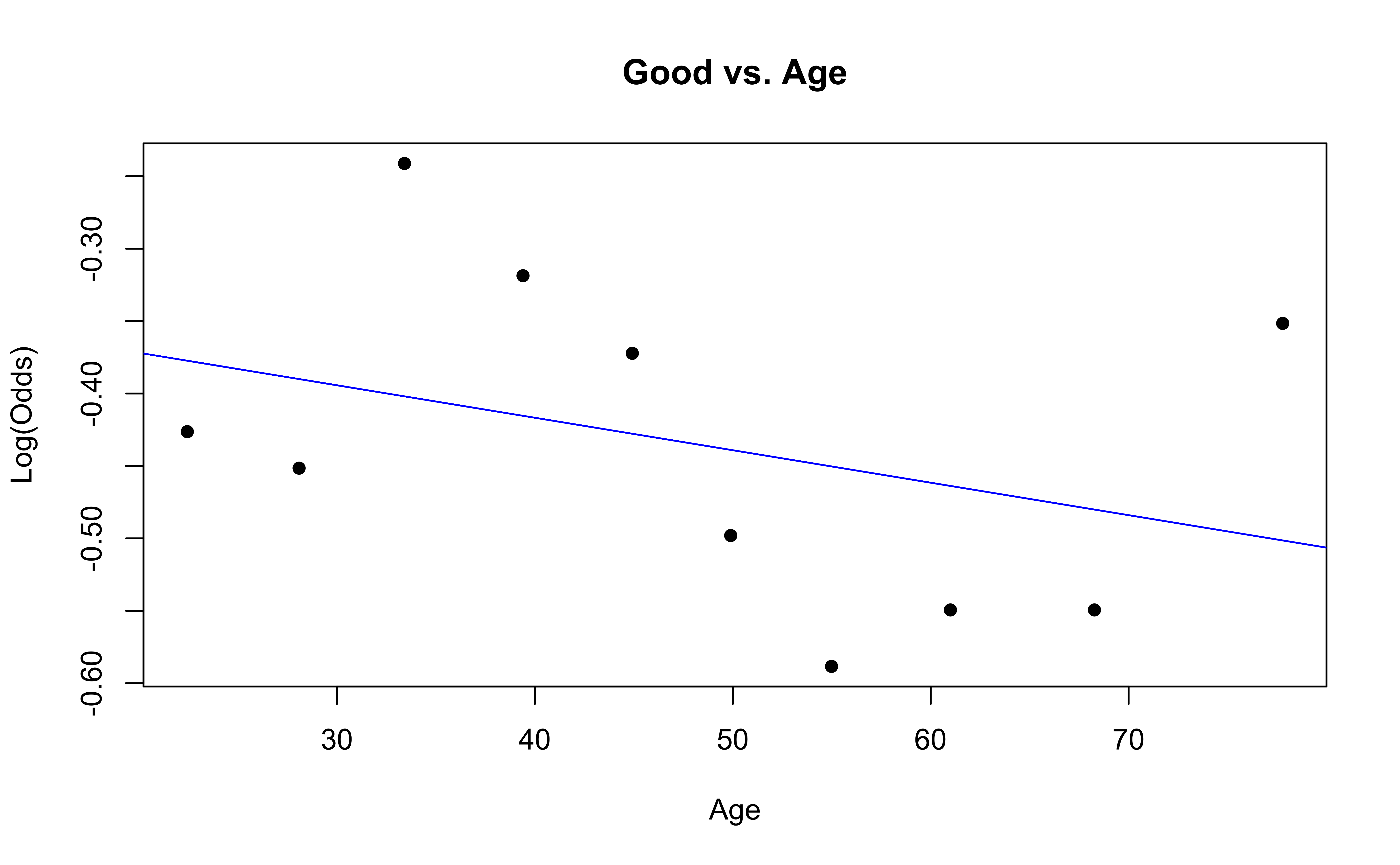
Similar to logistic regression, we will check linearity by examining empirical logit plots between each level of the response and the quantitative predictor variables.

nhanes_adult <- nhanes_adult %>%
  mutate(
    Excellent = factor(if_else(HealthGen == "Excellent", "1", "0")),
    Vgood = factor(if_else(HealthGen == "Vgood", "1", "0")),
    Good = factor(if_else(HealthGen == "Good", "1", "0")),
    Fair = factor(if_else(HealthGen == "Fair", "1", "0")),
    Poor = factor(if_else(HealthGen == "Poor", "1", "0"))
  )

Checking linearity

emplogitplot1(Excellent ~ Age, data = nhanes_adult, 
              ngroups = 10, main = "Excellent vs. Age")
emplogitplot1(Vgood ~ Age, data = nhanes_adult, 
              ngroups = 10, main = "Vgood vs. Age")

Checking linearity

emplogitplot1(Good ~ Age, data = nhanes_adult, 
              ngroups = 10, main = "Good vs. Age")
emplogitplot1(Fair ~ Age, data = nhanes_adult, 
              ngroups = 10, main = "Fair vs. Age")

Checking linearity

emplogitplot1(Poor ~ Age, data = nhanes_adult, 
              ngroups = 10, main = "Poor vs. Age")

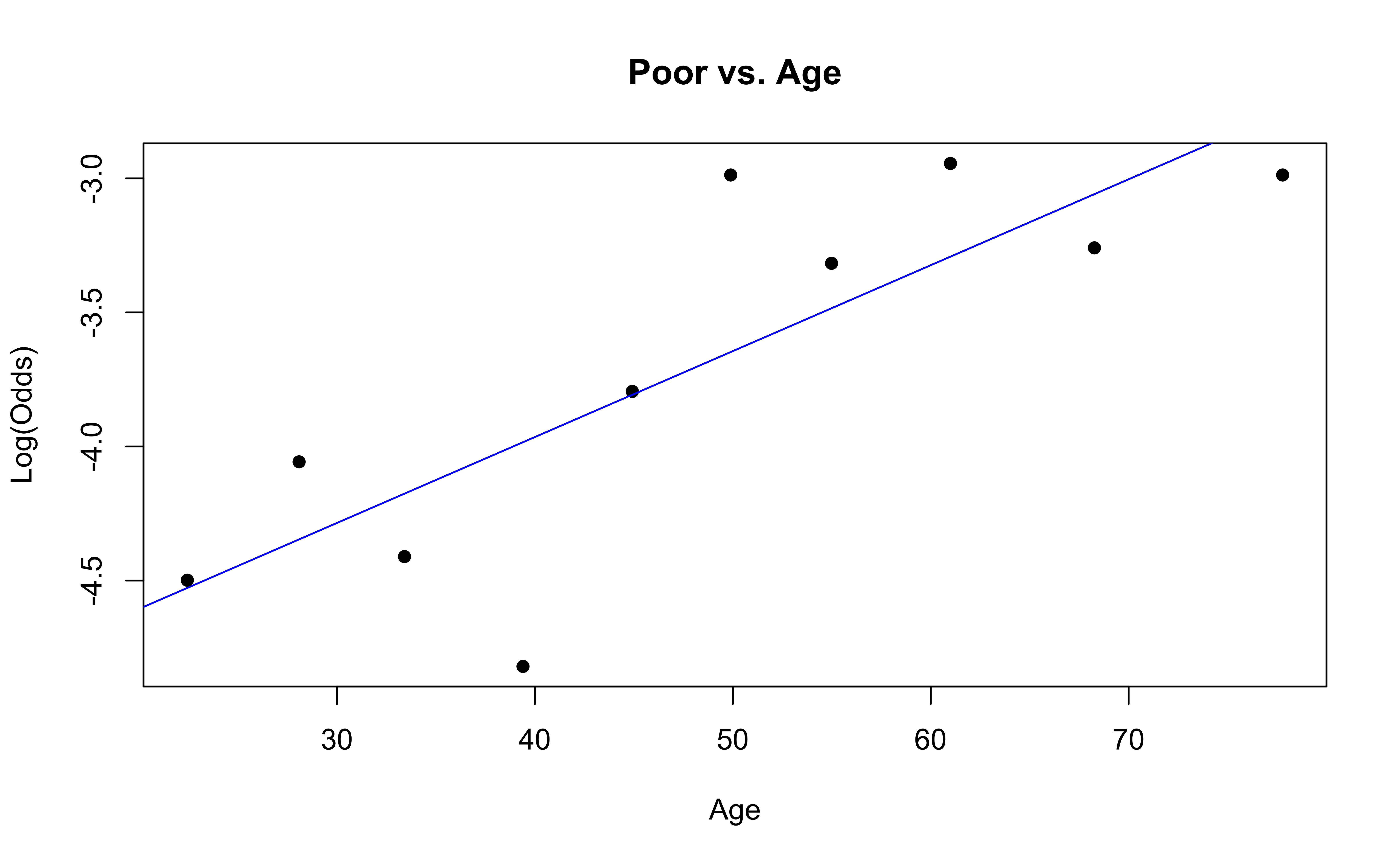
✅ The linearity condition is satisfied. There is a linear relationship between the empirical logit and the quantitative predictor variable, Age.

Checking randomness

We can check the randomness condition based on the context of the data and how the observations were collected.

  • Was the sample randomly selected?

  • If the sample was not randomly selected, ask whether there is reason to believe the observations in the sample differ systematically from the population of interest.

✅ The randomness condition is satisfied. We do not have reason to believe that the participants in this study differ systematically from adults in the U.S..

Checking independence

We can check the independence condition based on the context of the data and how the observations were collected.

Independence is most often violated if the data were collected over time or there is a strong spatial relationship between the observations.

✅ The independence condition is satisfied. It is reasonable to conclude that the participants’ health and behavior characteristics are independent of one another.

Recap

  • Predictions
  • Model selection for inference
  • Checking conditions for inference

sta210-s22.github.io/website