Multiple linear regression (MLR)

STA 210 - Spring 2022

Dr. Mine Çetinkaya-Rundel

Welcome

Announcements

  • Lab 3:

    • Any questions about lab / teamwork?
    • Due Friday, Feb 4 at 5pm

  • Exam 1:

    • Released Friday, Feb 4
    • Multiple choice questions (mostly conceptual) + open-ended exercises (like lab + homework)
    • Open book, open internet, open questions to me + Rick (head TA) only
    • No communication with others or posting questions on the internet allowed
    • What can you do to start preparing?

      • Review readings, assignments, feedback returned

      • Organize your notes

      • Come to office hours with questions

Computational setup

# load packages
library(tidyverse)   # for data wrangling and visualization
library(tidymodels)  # for modeling
library(openintro)   # for the duke_forest dataset
library(scales)      # for pretty axis labels
library(knitr)       # for pretty tables
library(patchwork)   # for laying out plots
library(GGally)      # for pairwise plots

# set default theme and larger font size for ggplot2
ggplot2::theme_set(ggplot2::theme_minimal(base_size = 20))

Considering multiple variables

House prices in Levittown

Analysis goals

  • We would like to use the characteristics of a house to understand variability in the sales price.

  • To do so, we will fit a multiple linear regression model.

  • Using our model, we can answers questions such as

    • What is the relationship between the characteristics of a house in Levittown and its sale price?
    • Given its characteristics, what is the expected sale price of a house in Levittown?

The data

levittown <- read_csv(here::here("slides/data/homeprices.csv"))
levittown
# A tibble: 85 × 7
   bedrooms bathrooms living_area lot_size year_built property_tax sale_price
      <dbl>     <dbl>       <dbl>    <dbl>      <dbl>        <dbl>      <dbl>
 1        4       1          1380     6000       1948         8360     350000
 2        4       2          1761     7400       1951         5754     360000
 3        4       2          1564     6000       1948         8982     350000
 4        5       2          2904     9898       1949        11664     375000
 5        5       2.5        1942     7788       1948         8120     370000
 6        4       2          1830     6000       1948         8197     335000
 7        4       1          1585     6000       1948         6223     295000
 8        4       1           941     6800       1951         2448     250000
 9        4       1.5        1481     6000       1948         9087     299990
10        3       2          1630     5998       1948         9430     375000
# … with 75 more rows

Variables

Predictors:

  • bedrooms: Number of bedrooms
  • bathrooms: Number of bathrooms
  • living_area: Total living area of the house (in square feet)
  • lot_size: Total area of the lot (in square feet)
  • year_built: Year the house was built
  • property_tax: Annual property taxes (in USD)

Response: sale_price: Sales price (in USD)

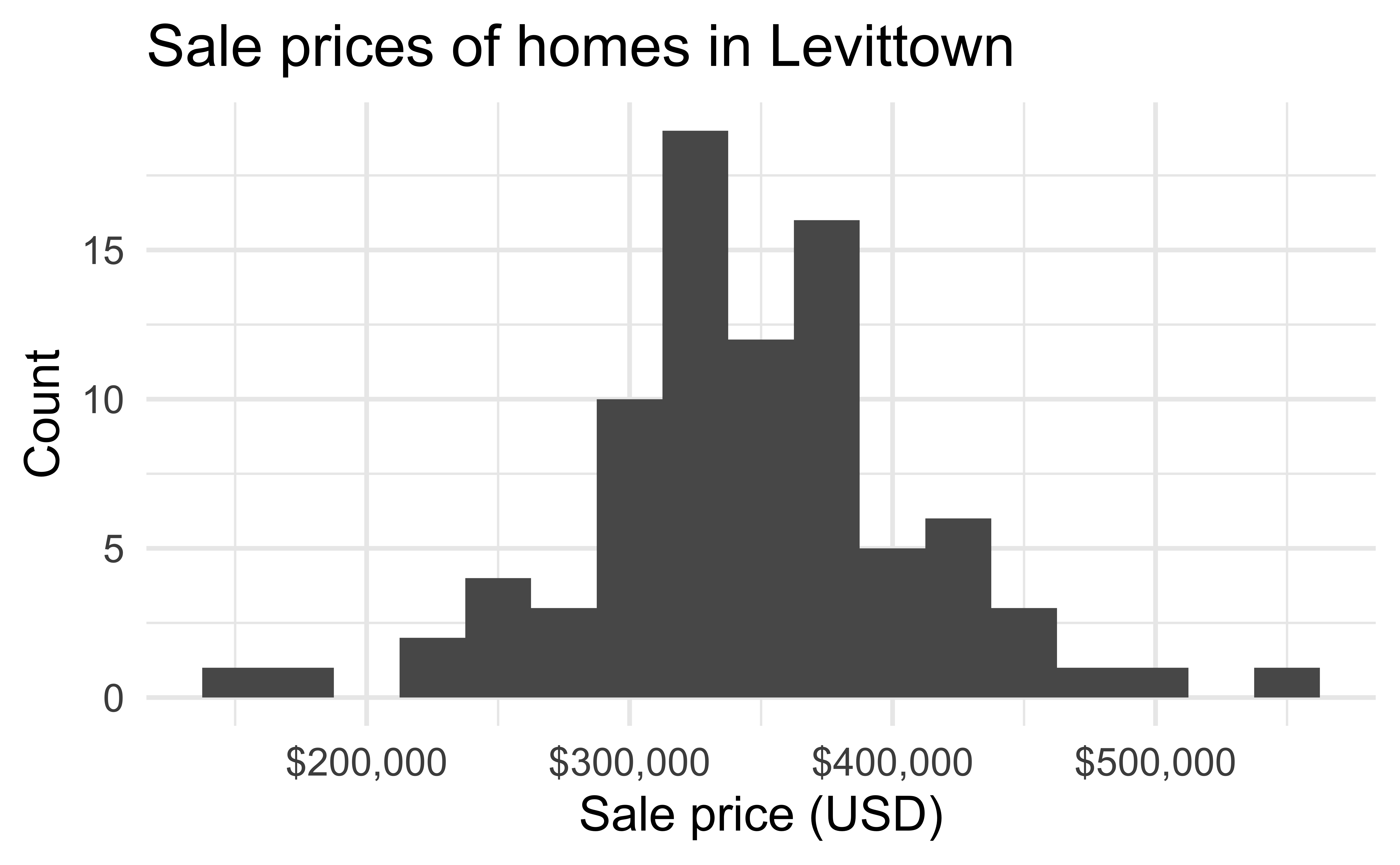
EDA: Response variable

EDA: Predictor variables

EDA: Response vs. Predictors

EDA: All variables

ggpairs(levittown) +
  theme(
    axis.text.y = element_text(size = 10),
    axis.text.x = element_text(angle = 45, size = 10),
    strip.text.y = element_text(angle = 0, hjust = 0)
    )

Single vs. multiple predictors

So far we’ve used a single predictor variable to understand variation in a quantitative response variable

Now we want to use multiple predictor variables to understand variation in a quantitative response variable

Multiple linear regression

Multiple linear regression (MLR)

Based on the analysis goals, we will use a multiple linear regression model of the following form

\[ \begin{aligned}\hat{\text{sale_price}} ~ = & ~ \hat{\beta}_0 + \hat{\beta}_1 \text{bedrooms} + \hat{\beta}_2 \text{bathrooms} + \hat{\beta}_3 \text{living_area} \\ &+ \hat{\beta}_4 \text{lot_size} + \hat{\beta}_5 \text{year_built} + \hat{\beta}_6 \text{property_tax}\end{aligned} \]

Similar to simple linear regression, this model assumes that at each combination of the predictor variables, the values sale_price follow a Normal distribution.

Regression Model

Recall: The simple linear regression model assumes

\[ Y|X\sim N(\beta_0 + \beta_1 X, \sigma_{\epsilon}^2) \]

Similarly: The multiple linear regression model assumes

\[ Y|X_1, X_2, \ldots, X_p \sim N(\beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_p X_p, \sigma_{\epsilon}^2) \]

The MLR model

For a given observation \((x_{i1}, x_{i2} \ldots, x_{ip}, y_i)\)

\[ y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \dots + \beta_p x_{ip} + \epsilon_{i} \hspace{8mm} \epsilon_i \sim N(0,\sigma_\epsilon^2) \]

Prediction

At any combination of the predictors, the mean value of the response \(Y\), is

\[ \mu_{Y|X_1, \ldots, X_p} = \beta_0 + \beta_1 X_{1} + \beta_2 X_2 + \dots + \beta_p X_p \]

Using multiple linear regression, we can estimate the mean response for any combination of predictors

\[ \hat{Y} = \hat{\beta}_0 + \hat{\beta}_1 X_{1} + \hat{\beta}_2 X_2 + \dots + \hat{\beta}_p X_{p} \]

Model fit

price_fit <- linear_reg() %>%
  set_engine("lm") %>%
  fit(sale_price ~ bedrooms + bathrooms + living_area + lot_size +
        year_built + property_tax, data = levittown)

tidy(price_fit) %>%
  kable(digits = 3)
term estimate std.error statistic p.value
(Intercept) -7148818.957 3820093.694 -1.871 0.065
bedrooms -12291.011 9346.727 -1.315 0.192
bathrooms 51699.236 13094.170 3.948 0.000
living_area 65.903 15.979 4.124 0.000
lot_size -0.897 4.194 -0.214 0.831
year_built 3760.898 1962.504 1.916 0.059
property_tax 1.476 2.832 0.521 0.604

Model equation

\[ \begin{align}\hat{\text{price}} = & -7148818.957 - 12291.011 \times \text{bedrooms}\\[5pt] &+ 51699.236 \times \text{bathrooms} + 65.903 \times \text{living area}\\[5pt] &- 0.897 \times \text{lot size} + 3760.898 \times \text{year built}\\[5pt] &+ 1.476 \times \text{property tax} \end{align} \]

Interpreting \(\hat{\beta}_j\)

  • The estimated coefficient \(\hat{\beta}_j\) is the expected change in the mean of \(y\) when \(x_j\) increases by one unit, holding the values of all other predictor variables constant.
  • Example: The estimated coefficient for living_area is 65.90. This means for each additional square foot of living area, we expect the sale price of a house in Levittown, NY to increase by $65.90, on average, holding all other predictor variables constant.

Prediction

What is the predicted sale price for a house in Levittown, NY with 3 bedrooms, 1 bathroom, 1,050 square feet of living area, 6,000 square foot lot size, built in 1948 with $6,306 in property taxes?


-7148818.957 - 12291.011 * 3 + 51699.236 * 1 + 
  65.903 * 1050 - 0.897 * 6000 + 3760.898 * 1948 + 
  1.476 * 6306
[1] 265360.4

The predicted sale price for a house in Levittown, NY with 3 bedrooms, 1 bathroom, 1050 square feet of living area, 6000 square foot lot size, built in 1948 with $6306 in property taxes is $265,360.

Prediction, revisit

Just like with simple linear regression, we can use the predict() function in R to calculate the appropriate intervals for our predicted values:

new_house <- tibble(
  bedrooms = 3, bathrooms = 1, 
  living_area = 1050, lot_size = 6000, 
  year_built = 1948, property_tax = 6306
  )

predict(price_fit, new_house)
# A tibble: 1 × 1
    .pred
    <dbl>
1 265360.

Confidence interval for \(\hat{\mu}_y\)

Calculate a 95% confidence interval for the estimated mean price of houses in Levittown, NY with 3 bedrooms, 1 bathroom, 1050 square feet of living area, 6000 square foot lot size, built in 1948 with $6306 in property taxes.


predict(price_fit, new_house, type = "conf_int", level = 0.95)
# A tibble: 1 × 2
  .pred_lower .pred_upper
        <dbl>       <dbl>
1     238482.     292239.

Prediction interval for \(\hat{y}\)

Calculate a 95% prediction interval for an individual house in Levittown, NY with 3 bedrooms, 1 bathroom, 1050 square feet of living area, 6000 square foot lot size, built in 1948 with $6306 in property taxes.


predict(price_fit, new_house, type = "pred_int", level = 0.95)
# A tibble: 1 × 2
  .pred_lower .pred_upper
        <dbl>       <dbl>
1     167277.     363444.

Cautions

  • Do not extrapolate! Because there are multiple predictor variables, there is the potential to extrapolate in many directions
  • The multiple regression model only shows association, not causality
    • To show causality, you must have a carefully designed experiment or carefully account for confounding variables in an observational study

Recap

  • Introduced multiple linear regression

  • Interpreted a coefficient \(\hat{\beta}_j\)

  • Used the model to calculate predicted values and the corresponding intervals

sta210-s22.github.io/website